January 11, 2012
A usable Karnaugh map
I am elated to see some activity lately with my career persuit this week. At least two people have called me about work about a resume on Dice.com I posted last year. It took a while, but I guess it is a resume on that site that I forgot to update recently. The information is still valid, but my most recent resume (which is not on Dice yet) is a bit more terse, in that everything important is on one page rather than two pages. On the other hand, this is a good thing for me. It means that there is an effective back up of the verbose version of my resume out there.
As much as I should take care of those matters immediately, there is still one outstanding project of which an important step will be completed tonight. There were two projects, but as you are about to see, see I finished one of these projects this afternoon and I hope to wrap up an important step for the other one tonight. I'll elaborate about what that project is when I'm finished.
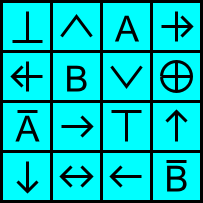
Tonight, I'm sharing the other thing I finished this afternoon that's I've been holding on to for about the past couple of months. Below the paragraph after this one is an improved Karnaugh Map or K-map for short. Normally, the chart explaining the K-Map is filled with either a list of numbers from 0 to 15 (or in their hexidecimal form of 0 through F), or binary values of zero and one that can alternately be described with a truth table.
My version replaces the list of numbers with a list of symbols that correspond with the various logical connectives. When arranged in specific order, their binary representation looks similar to the binary representation of hexidecimals or extended decimal numbers.
| K-Map | Truth Table | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
So basically, I've made made a K-map that crams in more information, and if you understand the order of numbers in a four element K-map, you can make this part of a cheat sheat where these symbols are on one side of a sticky note, and the various logical rules (which I've listed for conviencene below) on the other side.
| Statement | Proof |
|---|---|
| Ax(Ayz)=A(Axy)z | Associativity of Disjunction |
| Kx(Kyz)=K(Kxy)z | Associativity of Conjunction |
| Axy=Ayx | Commutativity of Disjunction |
| Kxy=Kyx | Commutativity of Conjunction |
| Kx(Ayz)=A(Kxy)(Kxz) | Distributivity of Conjunction over Disjunction |
| Ax(Kyz)=K(Axy)(Axz) | Distributivity of Disjunction over Conjunction |
| Ax0=x | Identity for Disjunction |
| Kx1=x | Identity for Conjunction |
| Kx0=0 | Annihator for Conjunction |
| Ax1=1 | Annihator for Disjunction |
| Axx=x | Idempotence of Disjunction |
| Kxx=x | Idempotence of Conjunction |
| Kx(Axy)=x | Absorption of Conjunction over Disjunction |
| Ax(Kxy)=x | Absorption of Disjunction over Conjunction |
| NNx=x | Double Negation |
| Kx(Nx)=0 | Complementation of Conjunction |
| Ax(Nx)=1 | Complementation of Disjunction |
| K(Nx)(Ny)=N(Axy) | de Morgan's Law |
| A(Nx)(Ny)=N(Kxy) | de Morgan's Law |
I know the notation may seem a bit akward, but I've put more than enough effort into this post. As much as I would like to put it in a familar mathematical notation, this is much faster to input into the computer at the moment.
Personally, I hope to use this K-map as logo for this website. I wonder if I can trademark it? Certainly you can still use it for academic purposes, but for my purpose, it would be used as a symbol for this website and my work here.


